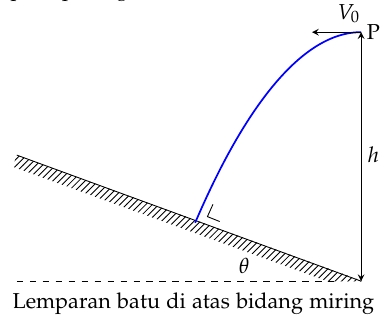
Tentukan kelajuan awal sebuah batu $latex V_0$ yang dilemparkan secara mendatar dari titik P, sehingga ia menumbuk bidang miring secara tegak lurus. Kemiringan bidang miring terhadap bidang mendatar adalah $latex \theta$, dan titik P berada pada ketinggian $latex h$ tepat di atas kaki bidang miring seperti pada gambar.
Pembahasan:
Jika kita anggap titik O=(0,0) adalah di tanah tepat di bawah titik P dan sumbu-$latex x$ positif mengarah ke kiri dan sumbu-$latex y$ positif mengarah ke atas maka persamaan gerak batu yang dilemparkan saat $latex t=0$ adalah
$latex x=V_0 . t~~~~~~~~~~~~(1)$
$latex y=h-\frac{1}{2}gt^2~~~~~~~~~(2) $
Pada saat menumbuk tegak lurus bidang miring batu membentuk sudut $latex \theta$ terhadap arah tegak, sehingga
$latex \tan\theta=\frac{V_{x}}{V_{y}}=\frac{V_0}{V_y}~~~~~~(3) $
dengan $latex V_x$ dan $latex V_y$ adalah komponen kecepatan batu saat menumbuk bidang miring dan karena $latex V_x$ selalu tetap maka $latex V_x=V_0$. Kita juga dapat memiliki persamaan kelajuan arah tegak yaitu
$latex V_y=gt~~~~~~~~~~~(4)$
dan kita dapat menggunakan persamaan $latex v^2=v_0^2+2as$ untuk sumbu tegak yaitu menjadi
$latex V_y^2=2g(h-y)=2g(h-x\tan\theta)~~~~~~~~~~~(5) $
dengan $latex y=x\tan\theta$ adalah ketinggian tempat tumbukan di bidang miring. Gunakan (3) dan (4) untuk mendapatkan
$latex t=\frac{V_0}{g\tan\theta}~~~~~~~~~~~~~~(6)$
lalu masukkan persamaan ini, (1) serta (4) ke dalam (5) sehingga menjadi
$latex g^2\frac{V_0^2}{g^2 \tan^2 \theta}=2g(h-\frac{V_0^2}{g}) $
yang akan menghasilkan
$latex V_0=\sqrt{\frac{2gh\tan^2\theta}{1+2\tan^2\theta}}$
Inilah nilai $latex V_0$ yang kita cari.

About the author