[latexpage]
Dua Katrol dan Bidang Miring. Dua buah massa disusun pada bidang miring yang tetap seperti pada gambar, $latex m_2$ besarnya adalah $latex \eta$ kali $latex m_1$. Jika seluruh permukaan licin dan anggap katrol memiliki massa yang dapat diabaikan, tentukan percepatan $latex m_2$!
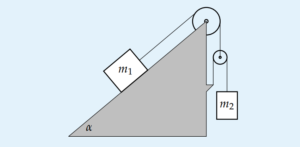
(Diambil dari Problems in General Physics, I.E. Irodov)
Penyelesaian :
Anggap $latex T_1, a_1$ dan $latex T_2,a_2$ berturut-turut adalah tegangan tali dan percepatan pada $latex m_1$ dan $latex m_2$. Persamaan gaya pada $latex m_1$ adalah
[latex]
T_1-m_1 g \sin\alpha=m_1a_1~~~~~~~~~~~~~~~~~~~~(1)\label{kiye1}
[/latex]
dan persamaan gaya pada $latex m_2$ adalah
[latex]
m_2g-T_2=m_2a_2.~~~~~~~~~~~~~~~~~~~~(2)\label{iki2}
[/latex]
Massa katrol dan gesekan yang diabaikan menghasilkan hubungan $latex T_1=2T_2$ dan konfigurasi katrol menyebabkan $latex a_2=2a_1$. Sehingga persamaan (2) dapat disubstitusikan dan dikalikan dua menjadi
[latex]
2m_2g-T_1=4m_2a_1~~~~~~~~~~~~~~~~~~~~(3)\label{kiye2}
[/latex]
lalu jumlahkan (1) dan (3) sehingga
[latex]
2m_2g-m_1g\sin\alpha=a_1(4m_2+m_1)[/latex]
[latex]a_1=g\frac{2m_2-m_1\sin\alpha}{4m_2+m_1}[/latex]
dan percepatan pada $latex m_2$ adalah
[latex]
a_2=2g\frac{2m_2-m_1\sin\alpha}{4m_2+m_1}
[/latex]

About the author